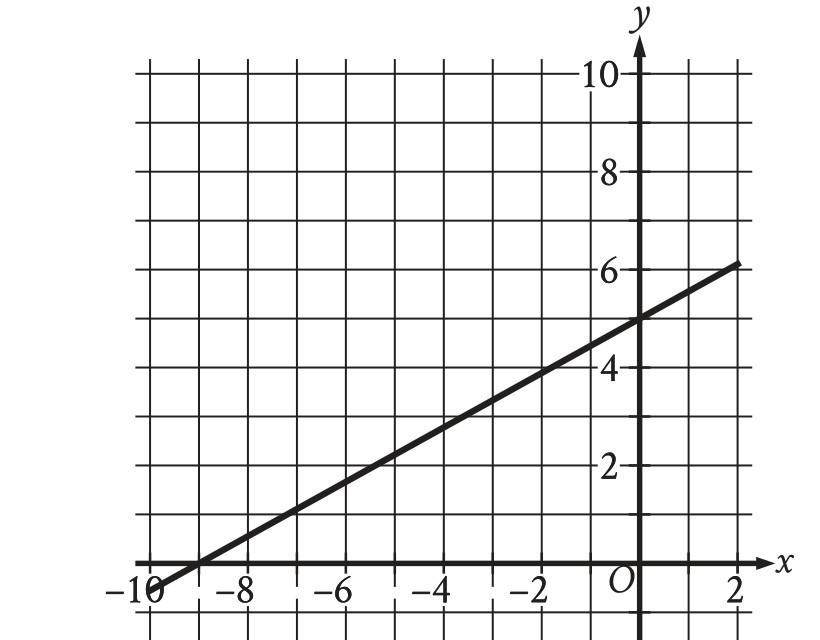
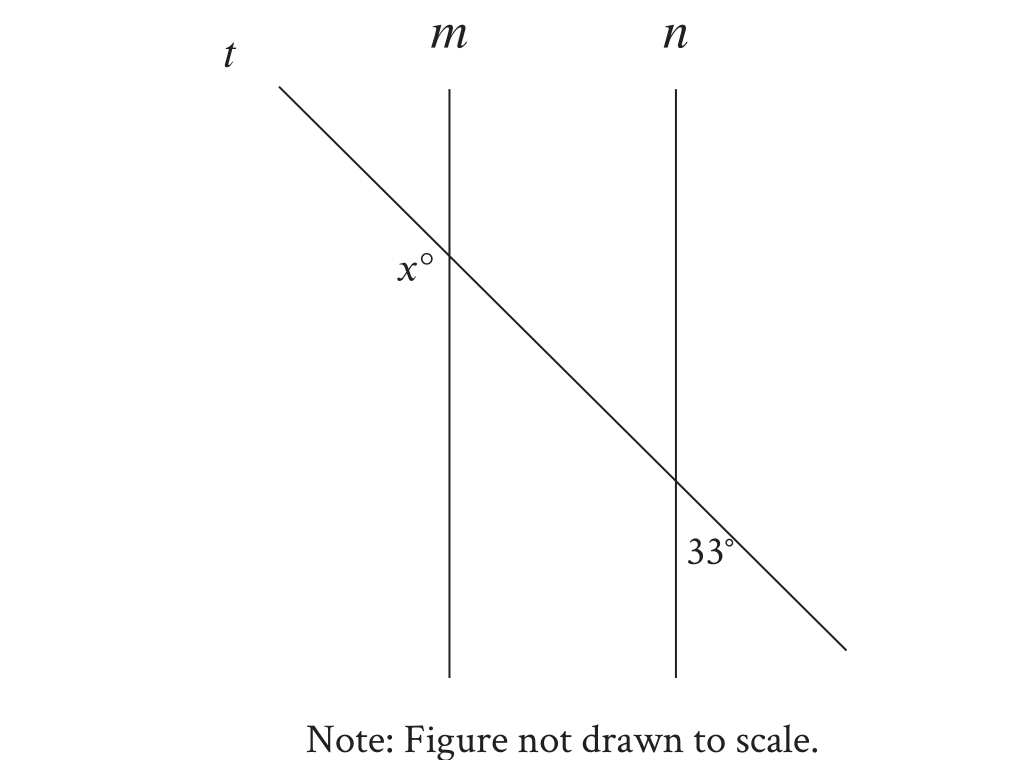
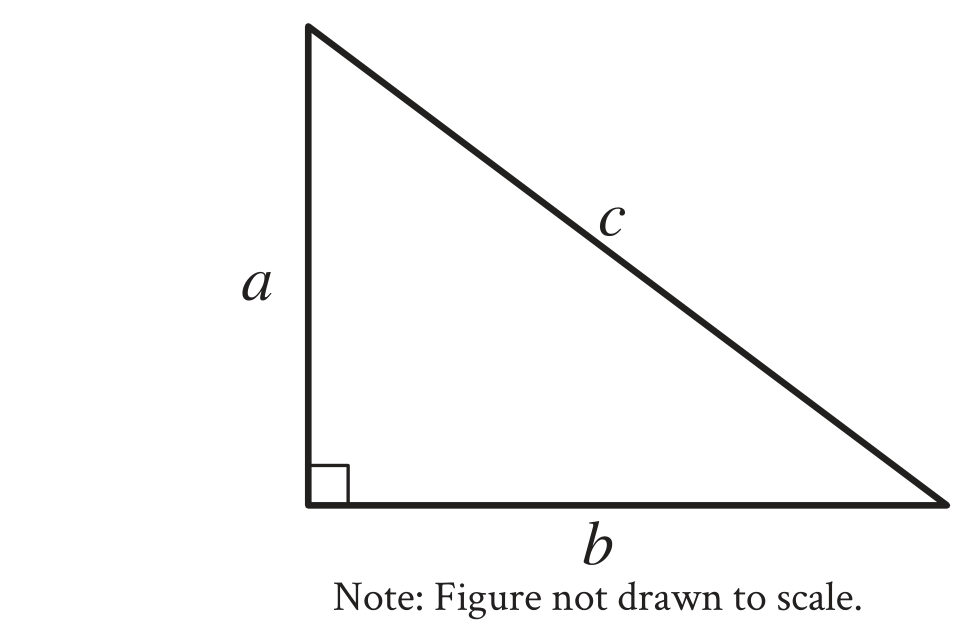
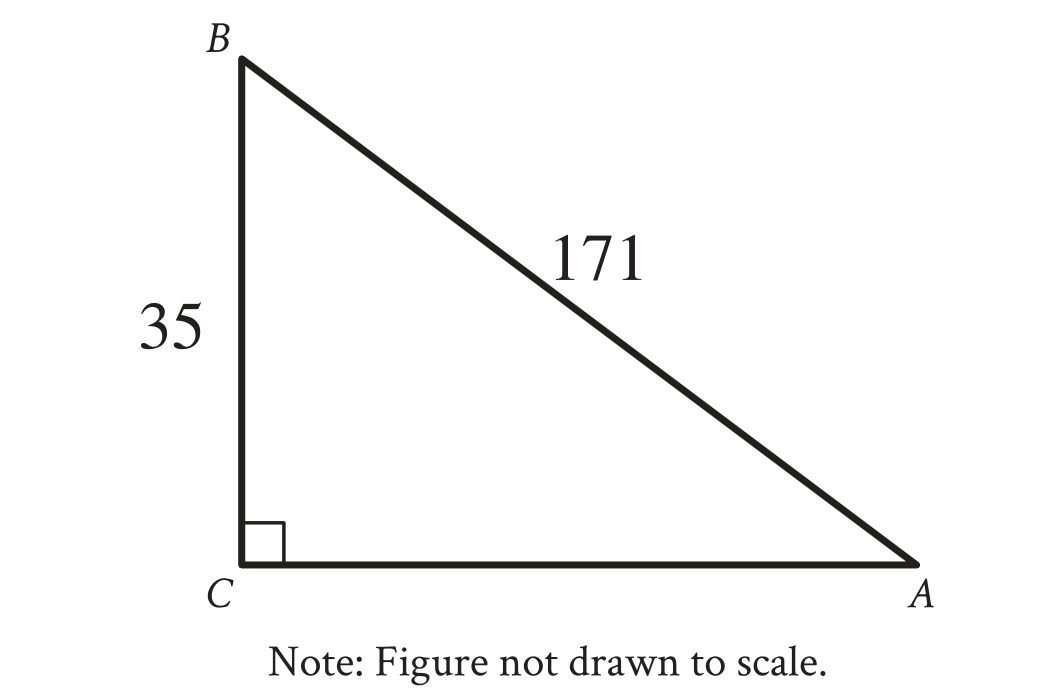
1
A bus is traveling at a constant speed along a straight portion of road. The equation \(d = 30t\) gives the distance \(d\), in feet from a road marker, that the bus will be \(t\) seconds after passing the marker. How many feet from the marker will the bus be 2 seconds after passing the marker?
A
30
B
32
C
60
D
90